Introduction
Global demand for energy is growing steadily, resulting in higher prices for fossil fuels, which represent the most important input for the energy industry. Sustainable energy sources currently provide 19 % of global energy consumption, and of this amount 50 % is generated from the combustion of plant biomass (REN21, 2013).
Many woody species grown in short rotation coppices (SRC) have gained importance in the supply of plant biomass (Hoogwijk, Faaij, Eickhout, de Vries, & Turkenburg, 2005). Among the most important wood energy species worldwide are eucalyptus (Eucalyptus globulus, E. nitens, E. denticulata) (Camps & Marcos, 2002), willow (Salix spp.), poplar (Populus spp.) and acacia (Acacia dealbata, A. melanoxylon, A. retinodes). These species have high productivity and can be promoted as fast-growing forest plants (Hoogwijk et al., 2005).
Evidence indicates that an important way to produce the biomass used in power generation is through the development of fast-growing plantations and short rotations. Interest in sprouting-generated stands lies mainly in the fact that they produce on average twice the volume of a sexual-regeneration stand in the first eight years (Sixto, Hernández, Barrio, Carrasco, & Cañellas, 2008) .
Biomass estimation is usually done using allometric models based on diameter at breast height (D) and total tree height (H), and occasionally some tree form measurements are also used (Clutter, Fortson, Pienaar, Brister, & Bailey, 1983). Allometric models have been developed for use in wood energy species grown in Africa (Henry et al., 2011), Europe (Muukkonen & Mäkipää, 2006) and South America (Návar, 2009). These models are based on characteristics easily measured on single-stem trees, such as the variables diameter at breast height and plant height, which together with the basic wood density should be related to biomass production (Hauk, Knoke, & Wittkopf, 2014).
However, in wood energy crops only the first rotation is formed by single-stem trees. From the second rotation onwards, numerous shoots emerge from each stump, which presents difficulties for predicting the total biomass yield in the aboveground part and its components. Therefore, it was decided to conduct a literature review with the objective of identifying species, rotation length and types of allometric models used to estimate biomass in SRC. For this reason, a bibliographic compiling of scientific publications related to the use of species, rotation length and allometric models for estimating aboveground biomass in SRC was performed.
Materials and methods
Creating the database
An online search was conducted of scientific journals included in the Scopus and Web of Science (WoS) databases. The review included all the recorded years of journals indexed in the two databases until April 2015. The general search criterion for the publications was short rotation coppice, and included the five following concepts: short rotation coppice (SRC), short rotation forestry (SRF), short rotation woody crops (SRWC), short rotation intensive culture (SRIC) and bioenergy crops (BC). These concepts were combined with the following five keywords: allometry, allometric, model, equation and partition, in order to increase the level of specificity in each of the five concepts related to the criterion of short rotation coppice.
Compilation and analysis of publications
All publications found for all possible combinations of the concepts and keywords were reviewed, excluding those publications that, despite matching the search criteria, lacked mathematical models for estimating biomass.
Documents obtained were exported to “EndNote X6” software, in order to join the two databases and remove duplicates automatically. The final database included only those publications in which the allometry mentioned was related to allometric models for estimating biomass produced by shoots in short rotation coppice systems.
Results and discussion
Using the criteria, concepts and simple and compound key words, defined for the study, 1,382 papers published between 1996 and 2015 were compiled. Most of the publications came from the Scopus database. The most frequently used concept was bioenergy crops, which allowed the identification of 492 publications (36 % of the total), of which 362 were obtained from the Scopus database and 130 from WoS. Another important concept was short rotation coppice, which recorded 420 publications (30 %), of which 282 were obtained from Scopus and 138 from WoS. The concepts that appeared with less frequency were short rotation forestry (260 publications), short rotation woody crops (140), short rotation intensive culture (42) and short rotation crops (28) (Table 1). The combination of the keyword (Model) with all concepts showed a greater record of publications in both databases (1,072 papers), but without the presence of allometric equations for estimating biomass (Table 1). After article purification, based on duplications and content type, only 65 publications that showed allometry aimed at estimating biomass were selected. Of these, 52 (82 %) were associated with the SRC concept and 13 (20 %) with the BC concept.
Table 1.
| Keyword | Concepts | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRC | SRF | SRWC | SRCR | SRIC | BC | |||||||
| Scopus | WoS | Scopus | WoS | Scopus | WoS | Scopus | WoS | Scopus | WoS | Scopus | WoS | |
| Allometry | 20 | 4 | 10 | 7 | 7 | 0 | 1 | 0 | 0 | 0 | 8 | 0 |
| Allometric | 22 | 11 | 17 | 12 | 7 | 5 | 2 | 1 | 2 | 0 | 4 | 1 |
| Model | 208 | 98 | 106 | 52 | 74 | 26 | 18 | 11 | 19 | 11 | 328 | 121 |
| Equation | 31 | 17 | 32 | 16 | 14 | 2 | 1 | 0 | 5 | 2 | 20 | 3 |
| Partition | 1 | 8 | 1 | 5 | 1 | 2 | 0 | 0 | 0 | 1 | 2 | 5 |
The 65 identified publications were examined in detail in order to select only those articles that explicitly showed models and variables for predicting shoot biomass in short rotation crops. Through this analysis only 25 publications were detected. Of these, a high number, 12 (48 %), were related to hybrid plantations of the genus Populus, which were established in countries such as Germany, Italy, Belgium, the Czech Republic, Denmark and France. The other publications were based on plantations of other plant genera, such as Salix (4 papers), established in Sweden, Denmark and Croatia, and Eucalyptus (2 papers) in Madagascar and France. There were also individual publications on mixed cultures of the genera Populus-Salix (Czech Republic), Liquidambar- Platanus (Georgia), Acer-Populus (Belgium), Alnus-Betula (Estonia), Daniellia (Benin), Platanus (USA) and Robina (Germany).
The genus Populus was the most common in the studies that generated allometric models to estimate aboveground shoot biomass (Table 2). Other plant genera important in developing SRC models are Salix and Eucalyptus. The studies were carried out with different clones, interspecific hybrids and a rotation length from one to 15 years.
Table 2.
| Model | Genus | Rotation length by year | Country | Source |
|---|---|---|---|---|
| 4 | Belgium | Vande Walle, Van Camp, Van de Castee le, Verheyen, and Lemeur (2007) | ||
| 4 | Belgium | Laureysens, Bogaert, Blust, & Ceulemans (2004) | ||
| 3 | Italy | Liberloo et al. (2005) | ||
| 3 | Italy | Liberloo et al. (2006) | ||
| 2 | Italy | Guidi, Piccioni, Ginanni, and Bonari | ||
|
|
2 and 3 | Belgium | Al Afas, Marron, Van Dongen, Laureysens, and Ceulemans (2008) | |
| 8 | Germany | Rock (2007) | ||
| 8 | Tanzania | Mugasha et al. (2013) | ||
| 8 | Czech Republic | Fischer, Trnka, Kučera, Fajman, and Žalud (2011) | ||
| 7 | Czech Republic | Fajman, Palát, and Sedlák (2009) | ||
| 2 and 3 | Denmark | Sevel, Nord-Larsen, and Raulund-Rasmussen (2012) | ||
| 8 | Estonia | Uri, Aosaar, Varik, and Kund (2010) | ||
|
|
8 | Georgia | Allen, Will, and Jacobson (2005) | |
| 3 | Belgium-France | Herve and Ceulemans (1996) | ||
| 2 | Sweden | Telenius (1999) | ||
|
|
2 | Croatia | (Bogdan, Kajba, & Katičić, 2006) | |
|
|
||||
|
|
3 | Benin | Avohou, Houehounha, Glele-Kakai, As sogbadjo, and Sinsin (2011) | |
|
|
||||
|
|
3 and 5 | Madagascar | Razakamanarivo, Razakavololona, Razafindrakoto, Vieilledent, and Albrecht (2012) | |
|
|
||||
|
|
(Bouvet, Nguyen-The, & Melun, 2013) | |||
|
|
1, 2, 3, 5, 6, 10, 13, 14 and 15 | France | ||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
7 | United States | Davis and Trettin (2006) | |
|
|
||||
|
|
4 | Germany | Röhle, Hartmann, Gerold, Steinke, and Schröder (2006) | |
|
|
||||
|
|
||||
|
|
||||
|
|
3 | Germany | Morhart, Sheppard, and Spiecker (2013) | |
|
|
||||
|
|
||||
|
|
||||
|
|
8 | France Brahim, Gavaland, and Cabanettes (2000) | France Brahim, Gavaland, and Cabanettes (2000) | |
|
|
||||
|
|
|
2, 3, 4 and 14 | Germany | Böhm, Quinkenstein, and Freese (2011) |
|
|
||||
|
|
|
1, 2 and 10 | Sweden | Verwijst and Telenius (1999) |
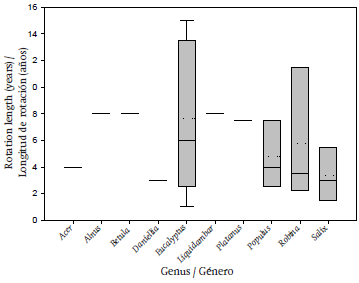
The rotation length used in the crops studied is very variable; in seven studies conducted with different plant genera, biomass was estimated at only a single rotation, as was the case of Acer, Alnus, Betula, Daniellia, Liquidambar and two in Platanus. Most of these were evaluated at age eight, except for Acer (4 years) and Daniellia (3 years). However, the genus Eucalyptus, reported in two studies, showed greater assessment variability over time (1, 2, 3, 5, 6, 10, 13, 14 and 15 years), followed by the genera Robina (2, 3, 4 and 14 years), Populus (3, 4 and 8 years) and Salix (1, 2, 4 and 6 years) (Figure 1).
It was found that different models are applied to estimate biomass in tree species from short rotation crops (Table 2), established mainly in the continents of Europe, Africa and North America, among which the typical exponential model y = b0Db1, tested in most species studied, except Eucalyptus, Alnus, Betula and Liquidambar, stands out. This model was used by Laureysens, Bogaert, Blust, and Ceulemans (2004), Liberloo et al. (2005), Liberloo et al. (2006), Rock (2007), Röhle, Hartmann, Gerold, Steinke, and Schröder (2006), Vande Walle, Van Camp, Van de Casteele, Verheyen and Lemeur (2007), Al Afas, Marron, Van Dongen, Laureysens, and Ceulemans (2008), Fajman, Palát, and Sedlák (2009), Avohou, Houehounha, Glele-Kakai, Assogbadjo, and Sinsin (2011), Fischer, Trnka, Kučera, Fajman, and Žalud (2011),Sevel, Nord- Larsen, and Raulund-Rasmussen (2012) and Mugasha et al. (2013), where some researchers measured each shoot as a single stem and others performed pruning on the stump, leaving one or two shoots, measuring stem diameter (D) at different heights depending on the species studied, in order to find the best model fit and thereby increase the level of correlation and accuracy of the estimates, which showed coefficients of determination (R2) greater than 0.85.
In willow (Salix), the biomass values obtained with the destructive method and those estimated with allometric equations (non-destructive) were compared. It was concluded that the exponential model y = b0Db1 was efficient and can be used in commercial willow plantations for estimating aboveground shoot biomass. Based on the results, the height with the greatest coefficient of determination was obtained by measuring the diameter of the stem at 105 cm (R2-adj ≥ 0.99), although heights of 85 and 55 cm (both with R2-adj ≥ 0.97) also showed acceptable prediction values and can be thus used when the crop is in its initial stage of development and has not reached one meter high. In Populus, Guidi, Piccioni, Ginanni and Bonari (2008) validated the exponential model to estimate the production of woody biomass and the amount of bark on the stem, based on its diameter at breast height (D), efficiently estimating the amount of total biomass with and without bark, as the best relationship between stem diameter and tree biomass.
The typical exponential model y = b0χb1 has been modified based on the results of different studies aimed at determining biomass with allometric relationships at different diameters (D), basal diameter (Db) and total height (H), used as predictive variables (χ) of the regression model. For example, Böhm, Quinkenstein, and Freese (2011), in Robinia pseudoacacia plantations, developed allometric equations to predict biomass based on basal diameter times total height (DbH). These equations were considered sufficiently accurate to estimate the woody biomass of the aboveground part of this species.
Other predictors frequently used in the models to es timate shoot biomass of the species studied are the natural logarithm of the diameter at breast height (lnD), diameter squared times height (D2H) and the ra tio (D/H), which range between three and four regres sion parameters.
On the other hand, Verwijst and Thelonious (1999) fitted the exponential model onto five different dates during the first growing season in Salix. Then they fitted the model intercept and determined the evolution of the slope (b1, b2) over the course of time T. The resulting model is y = (b0 + b1T + b2T2)Db3. T is expressed in relative terms and varies between 0 and 1, and D is the diameter at breast height. With this a coefficient of determination of R2= 0.99 is obtained (Table 2).
The linearized exponential model was one of the models studied in SRC. Morhart, Sheppard, and Spiecker (2013) evaluated in Populus maximowiczii × P. trichocarpa (hybrid 275) the logarithmic or linearized model lny = ln(b0) + biln(D), but according to Finney (1941) the result of transforming back the mean of the logarithms is to obtain the geometric mean of the original sample, which tends to underestimate the arithmetic mean of the population. Therefore, to correct the bias introduced into the model, they used the multiplicative correction factor (FC = e0.5∂ 2). After applying the factor (FC), they used the model ŷ = ˆb0D∂1FC to return to their original measurement scale. The adjusted coefficients of determination in the estimate (R2-adj) were 0.99 for the production of aboveground biomass in stems and leaves, while for branches a value of 0.98 was obtained. The researchers concluded that the proposed model, which uses diameter at breast height (D) as a predictor, provides an efficient and simple way to estimate aboveground biomass. Razakamanarivo, Razakavololona, Razafindrakoto, Vieilledent, and Albrecht (2012) also evaluated the linearized model to estimate aboveground and root biomass in Eucalyptu robusta, but with a different predictor lnyagb = b0 + b1ln(Dbi ), where (yagb) is the aboveground biomass and (Dbi) is stem basal diameter. For root biomass, they replaced within the model the dependent variable (ybgb) belowground biomass and stump circumference (Ciri) as the predictor variable. For correction of the logarithmic transformation bias, they applied the correction factor proposed by (Finney, 1941) (Table 2). Razakamanarivo et al. (2012) concluded that the evaluated model can be used to estimate aboveground and belowground biomass in E. robusta, using basal area and stump circumference respectively.
Brahim, Gavaland, and Cabanettes (2000) tested four generalized allometric regression equations to estimate the aboveground biomass in individual Populus trees. It was noted that the residual sums of squares were not significantly different when analyzing at site level, with a value for the coefficient of determination R2 higher than 0.94. The four models were acceptable for fitting the biomass estimate at site level, although it was established that the first three models tend to overestimate values when doing the analysis with all sites. Only the model y = b0 + b1D2m + b3 D2Hm showed significance with an R2 of 0.98 in estimating biomass in the combination of all sites, using as predictors the mean diameter (Dm) and diameter squared by mean total height (D2Hm) (Table 2). Results showed that the generalized regression with four parameters was sufficient to accurately estimate the aboveground biomass of trees grown at all sites.
Conclusions
In the compilation and descriptive analysis of scientific papers related to the use of allometric models for wood energy plantation shoots, the main plant species, rotations, methods and techniques used in estimating biomass in the SRC system were identified. In these papers the most frequently used genera are Populus, Salix and Eucalyptus. Most data sets in this analysis highlighted the exponential model, with different predictor variables, among which diameter at breast height (D), total height (H) and basal diameter (Db) were preponderant. Rotation length is highly variable from one to 15 years, mainly attributed to the geographical area and quality of the site where the crops were established.
