Introduction
Dynamic simulation is a technique that, in recent years, has been applied to mechanical and biological systems (Carcamo et al., 2014; Thornley & France, 2007). The simulation of a mathematical model allows understanding the behavior of a growth system of a given crop under different climatic or nutritional conditions (Soltani & Sinclair, 2012). This type of models are described by a set of dynamic equations in continuous or discrete form (Wallach, Makowski, Jones, & Bruns, 2014), and generally contain empirical knowledge, parameters and variables to explain crop yield (Bhatia, 2014; López-Cruz, Ramírez-Arias, & Rojano-Aguilar, 2005). In this sense, the use of crop simulation has made it possible to estimate and predict potential yields, as well as to control the factors that limit their production and profitability (Haefner, 2012; Radojevic, Kostadinovic, VlajKovic, & Veg, 2014).
In the specific case of tomato crops, because it is a biological system with chemical and physical interactions, which makes it highly non-linear, it is suitable for simulation analysis (Vargas-Sállago, López-Cruz, & Rico-García, 2012). This crop requires optimal climatic conditions to grow, mainly temperature, relative humidity, radiation and CO2 (Food and Agriculture Organization of the United Nations [FAO], 2001), and large amounts of water and nutrients are needed, particularly nitrogen, to achieve high yields (FAO, 2013). This commonly leads to nitrate leaching (NO3 -) and consequent groundwater pollution (Aristizábal-Gutiérrez & Cerón-Rincón, 2012; Gallardo et al., 2011).
Multiple dynamic mathematical models have been developed to estimate tomato growth, such as the following: TOMSIM, TOMGRO and TOMPOUSSE (López-Cruz et al., 2005; López-Cruz, Arteaga-Ramírez, Vázquez-Peña, López-López, & Robles-Bañuelos, 2009), which require a large number of state variables and parameters due to their structure in terms of ordinary non-linear differential equations (Wallach et al., 2014). In this study, the VegSyst model was used, which allows estimating crop biomass (DMP i ), plant nitrogen (N i ) and crop evapotranspiration (ET c ), and, considers thermal time and can be adapted to different sowing dates and different practices under greenhouse conditions. However, the model assumes that crops do not have water and nutrient limitations (Gallardo et al., 2011; Gallardo, Thompson, Giménez, Padilla, & Stöckle, 2014). Therefore, the objective of this study was to simulate and evaluate the VegSyst model to predict the growth of tomato crop and nitrogen content in the plant under greenhouse conditions.
Materials and methods
The VegSyst dynamic model was proposed by Gallardo et al. (2011) and has three input variables, thirteen parameters and three output variables in a set of difference equations in discrete time. It requires as input variables daily data on maximum temperature [Tmax (°C)], minimum temperature [Tmin (°C)] and photosynthetically active radiation [PAR (MJ·m-2·day-1)]. The model takes into consideration two stages in the crop cycle: 1) from transplanting to maximum PAR interception and 2) from maximum PAR interception to crop maturity (Giménez et al., 2013).
The dynamic model is written in difference equations in discrete form and uses the thermal time accumulation [CTT(i) (°D)], which is obtained by the triangulation method (Equation 1) proposed by Zalom, Goodell, Wilson, Barnett, and Bentley (1983) and retaken by Gallardo et al. (2011, 2014) and Giménez et al. (2013).
C T T ( i ) = 6 ( T m a x ( i ) - T l o w ) 2 T m a x ( i ) - T m i n ( i ) - 6 ( T m a x ( i ) - T u p ) 2 T m a x ( i ) - T m i n ( i ) 12
Where i is the day, Tmax (°C) and Tmin (°C) are the maximum and minimum daily temperature, respectively, and Tlow (°C) and Tup (°C) are the optimal maximum and minimum temperature levels, respectively, where growth does not stop, i.e. 12 and 28 °C, respectively, for tomato according to the FAO (2013).
To estimate the relative thermal time in the two stages of the crop (RTT), the VegSyst model uses the following equations (Gallardo et al., 2011, 2014; Giménez et al., 2013):
R T T 1 ( i ) = C T T ( i ) C T T f
R T T 2 ( i ) = C T T ( i ) - C T T f C T T m a t - C T T f
where CTT f is the cumulative of CTT(i) on the day the maximum PAR interception (°D) was observed and CTT mat is the value of CTT(i) on the day crop maturity (°D) was shown. The estimation of the intercepted fraction of PAR (f i-PAR ) in the two stages of the crop is carried out by means of Equations 4 and 5:
f i - P A R = f 0 + f f - f 0 1 + B 1 exp - α 1 R T T 1 i
f i - P A R = f f + f f - f m a t 1 + B 2 exp - α 2 R T T 2 ( i )
where f 0 is the initial fraction of PAR in the crop, f f is the maximum intercepted fraction of PAR, f mat is the fraction of PAR at crop maturity, α 1 and α 2 are fitting coefficients, B 1 and B 2 are functions estimated by Equation 6 and 7, where RTT 0.5 is the relative thermal time in the middle of the crop cycle.
B 1 = 1 e x p ( - α 1 R T T 0.5 )
B 2 = 1 e x p ( - α 2 R T T 0.5 )
From the above equations, Equation 8 is proposed for calculating daily dry matter in the crop [DMP i (g·m-2)].
D M P i = P A R i × R U E
Where PAR i is the daily PAR in the crop (MJ·m-2·day-1) calculated using the crop's f i-PAR product and the PAR measurements recorded by the sensor and RUE is the efficient use of radiation (g·MJ-1·PAR-1).
To estimate the nitrogen content in the plant [N i (%)] the model uses the following equation:
N i = a × D M P i b
Where a and b are fitting coefficients, and to estimate the nitrogen uptake by the plant (N upk (g·m-2)] we multiplied DMP i by N i .
The nominal values of Tup and Tlow were taken from FAO (2013), and CTT f and CTT mat were obtained from Equation 1. The other coefficients of Equations 1 to 9 are shown in Table 1, which were taken from Gallardo et al. (2011) and Giménez et al. (2013).
| Parameters | Value |
|---|---|
| Optimum maximum temperature ( |
28 °C |
| Optimum minimum temperature ( |
12 °C |
| Accumulation of thermal time at maximum PAR interception ( |
197 °D |
| Accumulation of thermal time at maturity of the crop ( |
461 °D |
| Efficient use of radiation ( |
4.3 |
| Fitting coefficient ( |
7.55 |
| Fitting coefficient ( |
-0.126 |
| Initial fraction of PAR in the crop ( |
0.02 |
| Maximum intercepted fraction of ( |
0.71 |
| Fraction of PAR at crop maturity ( |
0.65 |
| Relative thermal time in the first period of the crop cycle ( |
0.58 |
| Fitting coefficient ( |
9 |
| Fitting coefficient ( |
7 |
The variable daily dry matter was used to estimate plant height (H), number of fruits (Nfruits), number of nodes (Nnodes), dry matter of fruits (DMP Fruits ) and fresh weight of fruits (Pfreshfr). The equations for these variables were proposed based on the expo-linear and logistic model (Cárdenas, Giannuzzi, Noia, & Zaritzky, 2017; Posada & Rosero-Noguera, 2007):
H = D M P i × d d + d + D M P i e x p ( - e × t )
N f r u i t s = g 1 × D M P 1 + g 2 e x p ( - g 3 × t )
N n o d e s = h × A l t
D M P F r u i t s = c 1 × D M P
P f r e s f r = c 2 ( D M P F r u i t s × N f r u i t s )
where c 1 , c 2 , d, e, g 1 , g 2 , g 3 and h are fitting coefficients.
Regarding the variables of climate required by the VegSyst model, these were obtained through an Arduino™ card, which was programmed to acquire data from two sensors. The first one to measure temperature and relative humidity of the air, and the second to obtain PAR data. The characteristics of these sensors are shown in Table 2.
| Sensor | Manufacturer | Range | Accuracy |
|---|---|---|---|
| Temperature and humidity sensor | Grove Model: SEN51035P | Temperature: -40 a 80 °C | ± 0.3 °C |
| Humidity: 0 a 99.9 % | ± 3 % | ||
| PAR sensor | Spectrum Technologies Model: SP03668I6 | 0 to 2 500 µmol·m-2·s-1 | ± 5 % |
The temperature and humidity sensor was placed in the middle of a PVC (polymerizing vinyl chlorid) tube of 3 inches in diameter and 50 cm long, which was cover with aluminum foil and inside was placed a fan in the direction of extractor for air circulation and to prevent that radiation and heat generated by high temperatures affect the measurements. This served as a protection box for the sensors (Erell, Leal, & Maldonado, 2003, 2005; Lee et al., 2016). While the PAR sensor was installed on a metal base ensuring a 90° angle to the surface.
Climatic variables were measured with the sensors every 5 s and averaged every 5 min to store them in SD memory.
The equipment was installed in a commercial production greenhouse located in Aquixtla, Puebla, Mexico (19° 28’ 21” latitude north and 97° 33’ 10” longitude west, at 2 129 m altitude), with an area of 2 000 m2, with thermal tetra plastic cover with 15 % shade, zenithal ventilation and four side vents (with total area of 263 m2).
To evaluate the model, simulations and measurements of growth variables were compared in a crop of tomato (Solanum lycopersicum L.) hybrid saladette known as “Reserva”, of undetermined growth habit, grown in soil. The nutrients were applied in the irrigation water (fertigation). The crop data were taken during two agricultural cycles. The first, 150 days after transplanting (dat), from February to August 2016, and the second 31 dat, from August to December 2016. Sampling for the data was carried out every 15 days during the two growing cycles. The variables measured were: dry matter, nitrogen content, plant height, number of leaves, number of nodes, number of flowers and number of fruits.
In order to determine the dry matter, four plants were taken from each sample, which were subjected to a destructive process and then deposited in paper bags. Each sample was placed in a drying oven at 70 °C for 72 h, and then weighed to obtain the dry matter from the plant.
The nitrogen content in the plant was determined by the Kjeldhal method. For this purpose, 0.2 g of dry matter was taken from the plant and mixed with selenium, concentrated sulphuric acid, sodium hydroxide, 4 % boric acid, 0.1 % hydrochloric acid, methyl red and methylene red; the mixture underwent a digestion and distillation process (Jarquín-Sánchez, Salgado-García, Palma-López, Camacho-Chiu, & Guerrero-Peña, 2011). The nitrogen uptake was obtained by multiplying the nitrogen content by the dry matter content (Gallardo et al., 2011, 2014; Giménez et al., 2013).
Sensitivity analysis of the VegSyst model
The sensitivity analysis allows us to analyze the relationships between information entering and coming out of a model, as well as to evaluate input variables, parameters and initial conditions of the model with respect to state variables and outputs (López-Cruz, Rojano-Aguilar, Salazar-Moreno, & López-López, 2014; Saltelli, Tarantola, Campolongo, & Ratto, 2004). For this analysis, a local method was used (Equation 15), based on the estimation of partial derivatives (López-Cruz et al., 2014; Saltelli et al., 2004).
d d t ∂ x i ∂ p j = A t ∂ x ∂ p j + ∂ f ∂ p j j = 1 , … , q ; i = 1 , … , n
Where p is the nominal parameter, x is the vector of state variables, f is the model equations, q is the number of state variables, n is the number of parameters, and A(t) is equal to:
A t = ∂ f ∂ x = ∂ f i ∂ x i
By expressing the above equation in matrix form we have:
S ˙ = A S + M M = ∂ f i ∂ p j
The state sensitivity was estimated using Equations 18 to 20, and the absolute sensitivity using Equation 21.
d S ( t ) d t = A t , p 0 S t + M ( t , p 0 )
A t , p 0 = ∂ f ( x , u , p ) ∂ x | x = x t , p 0
M t , p 0 = ∂ f ( x , u , p ) ∂ p | x = x t , p 0
S t = ∂ x t , p 0 ∂ p (21)
Where p 0 is the nominal value of the parameters.
The sensitivity of the outputs and the relative sensitivity were estimated with Equations 22 and 23, respectively,
S y = ∂ y ∂ p = ∂ g ∂ x S + ∂ g ∂ p
S ( t ) = p 0 x t , p 0 ∂ x t , p 0 ∂ p
Sensitivity indices were obtained from the integral under the curve of the sensitivity functions (López-Cruz et al., 2014).
Calibration of the VegSyst model
The parameters of a mathematical model can be provided by its author, known through bibliography or must be determined from measurements (López-Cruz et al., 2009; Wallach et al., 2014). One of the best known techniques for finding parameter values is by estimation or calibration using the nonlinear least squares method (Levenberg-Marquardt) (Soltani & Sinclair, 2012). This technique involves an iterative process of convergence, where a function to be minimized is sought (Equation 24) and allows identifying the values of the parameters of the VegSyst model (López-Cruz et al., 2009). The non-linear least squares procedure is available in the function “lsqnonlin” of Matlab®.
f x = 1 2 ∑ j = 1 m r j 2 ( x )
Where x = x 1 …x n and r j = r 1 (x 1 )…r n (x m ) are residual values under the condition m ≥ n; r(x) = [r 1 (x 1 )…r n (x m )].
While the Jacobian matrix has the following structure:
J x = ∂ r j ∂ x i , 1 ≤ j ≤ m , 1 ≤ i ≤ n
∇ f x = 1 2 ∑ j = 1 m r j x ∇ r j x = J x T r x
∇ 2 f x = J x T J x + ∑ j = 1 m r j x ∇ 2 r j x
If r j s ≈ ∇ 2 r j (x) or residues r j (x) are small, then:
∇ 2 f x = J x T J x
x i + 1 = x i - λ ∇ f (29)
In order to quantitatively evaluate the behavior of the VegSyst model before and after calibration, the following statistics were obtained: determination coefficient (R2), mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), mean of difference between measured and estimated data (BIAS), coefficient of variation (CV) and variance (VAR) (Wallach et al., 2014).
Results and discussion
To perform the simulation with the VegSyst model, calibration and model validation techniques must be used (Giménez et al., 2013), because when using parameters proposed for other study areas, the simulations do not match the measurements made in the crop. For this reason, the sensitivity analysis and the calibration of the model were carried out. The first technique is used to determine how the variables predicted by the model are affected by the uncertainty of the parameters (López-Cruz et al., 2014), and with the second technique the values of those parameters are found (Soltani & Sinclair, 2012).
Sensitivity analysis of the VegSyst model
Equations 15 to 23 were applied together with the variables of climate of the first agricultural cycle to perform the sensitivity analysis of the VegSyst model in the two stages of the crop, and in the variables of dry matter and nitrogen content in the plant. Sensitivity analysis was not performed for Equations 10 to 14, because they are fitting parameters and must be identified by calibration. To determine the sensitivity indices, the nine parameters were plotted with each output variable for the two growing cycles, and the integral was calculated under the curve for each parameter using the function “trapz” Matlab® (Table 3).
| Parameter |
|
|
||
|---|---|---|---|---|
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | |
| 121 | 121 | 45.98 | 45.98 | |
| 0 | 0 | 121 | 121 | |
| 0 | 0 | 288.1 | 291.2 | |
|
|
120.99 | 246.76 | 45.97 | 82.07 |
|
|
0.0029 | 0 | 0.001 | 0 |
|
|
0 | 94.97 | 0 | 36.09 |
|
|
0.36 | 1.89 | 0.14 | -0.71 |
|
|
0.46 | 0 | 0.178 | 0 |
|
|
0 | 0.31 | 0 | 0.12 |
The magnitude of each parameter with respect to each variable (Table 3) allows determining that RUE, a, b, f f and f mat are the most sensitive of the model in the two output variables and, therefore, they are the ones that must be calibrated, while the other four can take nominal values proposed by the authors of the model (López-Cruz et al., 2014; van Straten, 2008).
Calibration of the VegSyst model
Using the nonlinear least squares technique and the Levenberg-Marquardt algorithm, the values of the five most sensitive parameters of the VegSyst model (RUE, a, b, f f and f mat ) were found and, additionally, the eight fitting parameters of Equations 10 to 14 were found (Table 4).
| Parameters | Before calibration | After calibration in the first growing cycle | After calibration in the second growing cycle |
|---|---|---|---|
| 4.3 | 4.19 | 4.01 | |
| 7.55 | 7.66 | 7.93 | |
| -0.126 | -0.22 | -0.24 | |
|
|
0.71 | 0.69 | 0.716 |
|
|
0.65 | 0.89 | 0.89 |
|
|
0.005 | 0.079 | 0.01 |
|
|
0.01 | 0.049 | 0.037 |
| -2 | -2 | -2.2 | |
| -0.02 | -0.02 | -0.04 | |
|
|
0.03 | 0.049 | 0.047 |
|
|
9 | 10 | 9.94 |
|
|
0.1 | 0.05 | 0.07 |
| 0.1 | 0.13 | 0.12 |
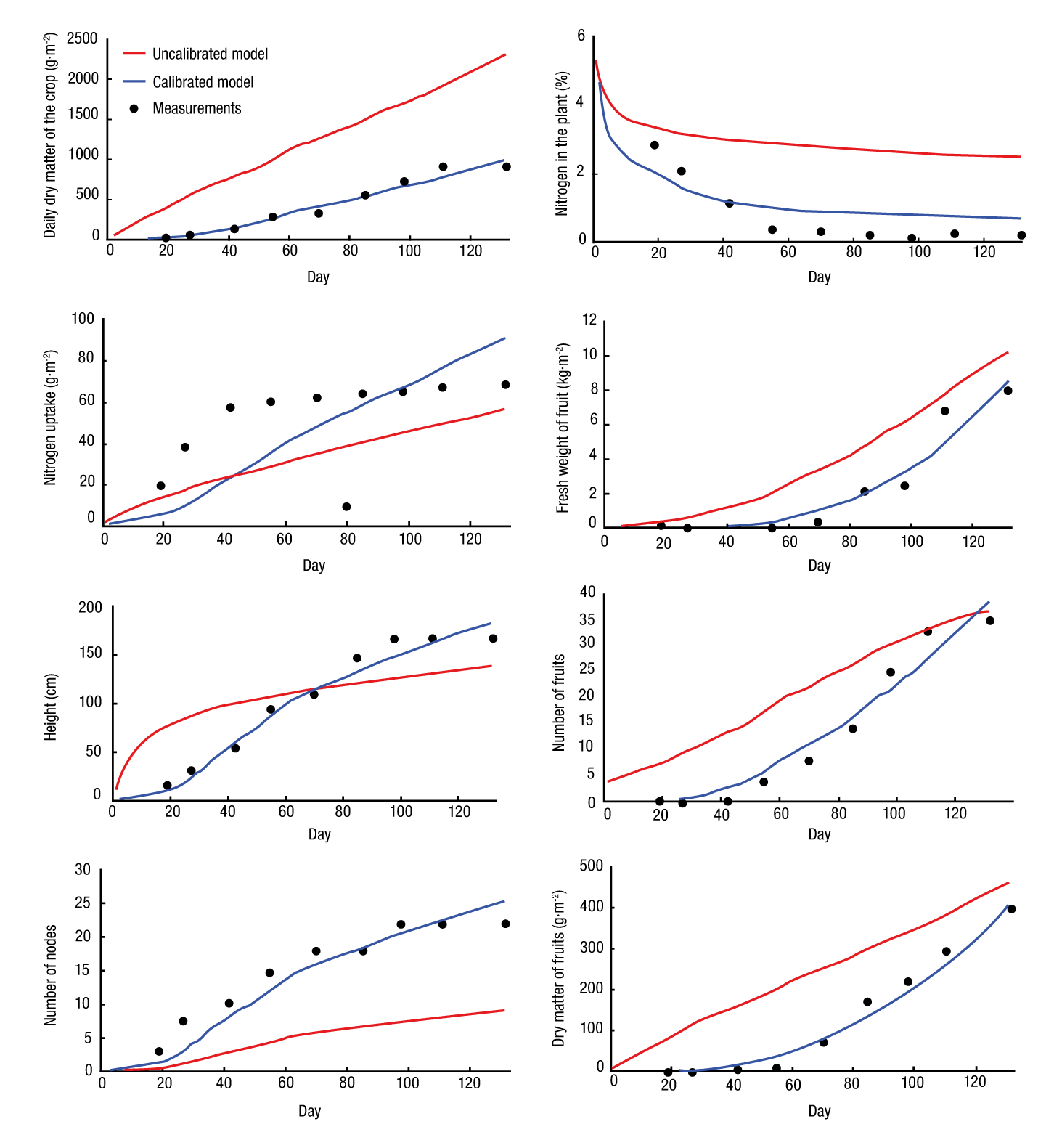
The simulations before and after calibration for the first and second growing cycle are shown in Figures 1 and 2, respectively; for both fitting was obtained after calibration.
Table 5 shows the values of the statistics determined to evaluate the behavior of the VegSyst model before and after calibration.
|
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| R2 | 0.9629 | 0.9673 | 0.88 | 0.97 | 0.71 | 0.67 | 0.88 | 0.93 |
| MSE | 780910 | 3588.7 | 4.26 | 0.31 | 530 | 400.58 | 4.70 | 0.55 |
| RMSE | 883.68 | 59.905 | 2.06 | 0.56 | 23 | 20.01 | 2.16 | 0.74 |
| MAE | 834.01 | 44.292 | 1.95 | 0.52 | 21.43 | 17.28 | 1.87 | 0.48 |
| BIAS | 834.01 | 4.9045 | 1.95 | 0.22 | 21.43 | 9.73 | 1.87 | 0.045 |
| CV | 0.5397 | 0.7848 | 0.16 | 0.40 | 0.47 | 0.34 | 0.83 | 1.23 |
| VAR | 413730 | 103140 | 0.215 | 0.2 | 236.24 | 211.3 | 10 | 6.51 |
| R2 | 0.9532 | 0.970 | 0.91 | 0.96 | 0.95 | 0.95 | 0.91 | 0.97 |
| MSE | 1508.2 | 108.92 | 99.49 | 32.92 | 115.25 | 5.45 | 17647 | 505.62 |
| RMSE | 38.83 | 10.43 | 9.97 | 5.73 | 10.73 | 2.33 | 132.84 | 22.48 |
| MAE | 34.48 | 8.98 | 8.67 | 2.43 | 10.05 | 2.02 | 126.27 | 18.86 |
| BIAS | 6.18 | 3.24 | 8.67 | 0.53 | 10.05 | 1.01 | 126.27 | 113.73 |
| CV | 0.25 | 0.624 | 0.50 | 0.94 | 0.62 | 0.60 | 0.54 | 1.07 |
| VAR | 738.71 | 3621 | 112.2 | 101.27 | 9.05 | 69.57 | 16549 | 15899 |
The results shown in Table 5 indicate that there was fitting of the output variables. The MSE decreased after calibration, i.e. the average of squared errors decreased between measurements and simulations (Soltani & Sinclair, 2012). The RMSE showed a similar situation for the eight estimated variables. For its part, the MAE value after calibration indicated that there was a fitting after calibration (Wallach et al., 2014). According to Soltani and Sinclair (2012), the value of BIAS should be close to zero and that of R2 close to 1, values similar to those obtained in this study. The CV decreased only for N upk and Nnodes with respect to those shown before the calibration. The statistical value of the VAR decreased for DMP i , N i , N upk , Pfreshf, Nfruits and DMP Fruits , which indicates these variables were fitted.
To determine which of the two sets of parameters obtained in model calibration predicts crop growth, a cross validation (Vehtari, Gelman, & Gabry, 2017) was performed between the first cycle parameter set and the second cycle simulation data, and vice versa. The statistical results of this validation are shown in Table 6.
|
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| SC1 | SC2 | SC1 | SC2 | SC1 | SC2 | SC1 | SC2 | |
| R2 | 0.9673 | 0.9732 | 0.96 | 0.896 | 0.697 | 0.844 | 0.938 | 0.978 |
| MSE | 4013 | 2505 | 0.29 | 0.495 | 580.91 | 458.92 | 0.622 | 0.157 |
| RMSE | 63.3509 | 50.0505 | 0.54 | 0.703 | 24.10 | 21.42 | 0.788 | 0.397 |
| MAE | 48.8829 | 39.9663 | 0.50 | 0.643 | 21.02 | 29.84 | 0.463 | 0.269 |
| BIAS | 20.2339 | 7.4181 | 0.26 | 0.122 | 19.97 | 18.73 | 0.025 | 0.083 |
| CV | 0.8016 | 0.7372 | 0.43 | 0.400 | 0.691 | 0.616 | 1.187 | 1.163 |
| VAR | 100170 | 84389 | 0.25 | 0.194 | 616.04 | 492.4 | 5.727 | 3.424 |
| R2 | 0.958 | 0.9723 | 0.958 | 0.9347 | 0.937 | 0.947 | 0.973 | 0.988 |
| MSE | 398.37 | 868.51 | 247.73 | 307.32 | 10.025 | 7.699 | 1777 | 450.33 |
| RMSE | 19.95 | 29.470 | 15.73 | 17.53 | 3.166 | 2.774 | 42.156 | 21.221 |
| MAE | 12.79 | 25.939 | 2.907 | 3.018 | 2.781 | 2.442 | 26.520 | 17.039 |
| BIAS | 7.147 | 25.939 | 2.17 | 2.5096 | 1.667 | 2.245 | 114.38 | 114.92 |
| CV | 0.678 | 0.599 | 0.905 | 0.905 | 0.678 | 0.599 | 1.098 | 1.049 |
| VAR | 5182 | 3142 | 172.44 | 91.06 | 74.63 | 53.111 | 23863 | 13104 |
With the simulation of the second cycle using parameters of the first cycle (SC2) a better yield was obtained in all the statistics for the variables DMP i , N upk , Pfreshf, Nnodes and DMP Fruits , while for N i , H and Nfruits the highest statistical yield with both sets of parameters was alternated (Table 6). Therefore, it is not possible to say that the set of parameters of the first growing cycle is the one that validates the model for future experiments; therefore, these parameters should be chosen from the ranges shown in Table 4.
To determine whether the model predicts the variables tomato crop grow and nitrogen content in the plant, R2 was compared before calibration and after cross validation (Table 7). With this analysis it could be stated that R2 after calibration and cross validation can be predicted at 95 % in plant dry matter, nitrogen in the plant, fresh weight of fruits, height of the plant, number of fruits, number of nodes and dry matter of fruits, and at 84 % nitrogen uptake.
| Growth variable | Before calibration | SC11 | SC2 |
|---|---|---|---|
| Plant dry matter | 0.962 | 0.967 | 0.973 |
| Nitrogen in the plant | 0.88 | 0.960 | 0.896 |
| Nitrogen uptake | 0.71 | 0.697 | 0.844 |
| Fresh weight of fruits | 0.88 | 0.938 | 0.978 |
| Height | 0.95 | 0.958 | 0.972 |
| Number of fruits | 0.91 | 0.958 | 0.934 |
| Number of nodes | 0.95 | 0.937 | 0.947 |
| Dry matter of fruits | 0.91 | 0.973 | 0.988 |
Conclusions
The VegSyst model and the equations proposed, based on the expo-linear and logistic model, allow to simulate, evaluate and estimate growth variables of tomato crop and nitrogen content in the plant at 95 %. Moreover, the sensitivity analysis allowed identifying the parameters that most contribute to the VegSyst model, and with the technique of non-linear least squares the simulations and measurements made in the crop were fitted.








 Previous article
Previous article